Division Algebra Over The Reals

Over the complex numbers the only normed division algebra is the algebra of complex numbers themselves. What are the other examples of Central divison algebras over mathbbQ with the same property.

In This Precalculus Lesson For Inverse Trig Functions Your Students Will Relate Inverse Properties To T Precalculus Trigonometric Functions Smart Board Lessons

The study of real division algebras was initiated by the construction of the quaternion and the octonion algebras in the mid-19th century.

Division algebra over the reals. In spite of its long history the problem of classifying all finite-dimensional real division algebras is still unsolved. And further apply the normed division algebra concepts to quaternions. The fields of meromorphic functions on connected.

Hav-ing completed our introduction to normed division algebras we then define the octonions using their most standard construction as a vector space over the reals. The problem of real division algebra is to show that there. This algebra can be algebraic.

For any you have unique elements and unless. The next step are the Sedenions S which are no longer a division algebra but still power-associative. A division algebra over the real numbers R is a division ring that has the reals as a subfield.

The Hurwitz theorem says that over the real numbers there are up to isomorphism exactly four finite-dimensonal normed division algebras. De nition Real Division Algebra Let A eb an algebra over R not on-c taining only of its zero-element. From C we get HwhichisnolongercommutativeandthenwegetOwhichisnolongerassociative.

Frobenius proved in 1877 that the only division algebras over R of finite dimension are a R itself of dimension 1 b the complex numbers C a field of dimension 2 over R and c the quaternions H a skew field of dimension 4 over R. This is an old result proved by Frobenius but I cant remember how the. 3028 13 13 silver badges 24 24 bronze badges endgroup 4.

Brief Division in Algebra video. Follow asked Oct 3 15 at 1212.

Or get the full course http. Division algebra An algebra over a field such that for any elements and the equations are solvable in. The Frobenius theorem states that a nite dimensional division algebra over the reals is one of the reals R the complex numbers C or the quaternions H.

This division algebra is of dimension 16. If the division algebra is called a central division algebra. The first example of a finite dimensional central division algebra which is not a crossed product with cyclic Galois group was found by AA.

Here a division algebra is an associative algebra where every nonzero number is invertible like a field but without assuming commutativity of multiplication. A division algebra over a field is a -algebra which allows division ie. An associative division algebra considered as a ring is a skew-field its centre is a field and.

Hurwitzs theorem says all 8-dimensional normed division algebras over the reals are nonassociative and isomorphic to the octonions. Recently Peter Freyd showed me a proof that is simpler than the known proofs. 1 day agoQuaternions over mathbbQ are an example of a Central Division algebra over mathbbQ for which the basis elements ijij other than 1 are represented by skew-symmetric matrices in regular representation.

ON THE FROBENUIS THEOREM ON REAL DIVISION ALGEBRAS MICHAEL BARR 1. Assuming the dimension is. We apply the normed division algebra concepts to the octonions.

Conjugation as involution while we loose the property of being real. Can we cosntruct an infinite dimensional division algebra over the reals. 2 begingroup Fields of rational functions.

In short the author claims to have found an 8-dimensional normed division algebra over ℝ mathbbR but there is no such thing. A is a aler division algebra if for any a A and any non-zero b A there exists exactly on x and y in A such that a bx and a yb This de nition does not assume that the algebra A is either commutative or as-sociative. We can go on forever doubling in each step the dimension of the algebra.

Any finite dimensional central simple algebra over afield of algebraic numbers is isomorphic to a crossed product with a cyclic Galois group. Why are the only associative division algebras over the real numbers the real numbers the complex numbers and the quaternions. The notation means that is an element such that.

This famous result published in 1923 has been confirmed with a number of well. An associative algebra over a field is a -algebra in which the multiplication is associative what else. We review the theory of this problem with focus on recent contributions.

Solving Equations By Distributive Property Solutions Examples Videos

So Learnin For Ya Cuz Your Brain Needs It Today Physics Math Methods Math

25 Geeky Math Jokes To Celebrate Pi Day Math Jokes Math Humor Math Memes

Real Numbers Precalculus School Yourself

The Best Way Of Understanding Is Every Irrational Number A Real Number Or The Best Answer For The Query That Real Numbers Irrational Numbers Real Number System

Normed Division Algebra In Nlab

Interactive Bulletin Board Sorting Real Numbers Headers And Reals Numbers Are A Part Of The Number System Bundle Number Sense Real Number System Common Core

Multiplying And Dividing Rational Expressions 3 Rational Expressions Math Videos Algebra Ii

Graphs Of Rational Functions Precalculus Unit 2 Distance Learning Rational Function Smart Board Lessons Precalculus

Order Of Operations Find The Mistake Cards Order Of Operations Math Operations Basic Math

For Realz Math Jokes Math Puns Math Humor

The Hierarchy Of Numbers Learnist Complex Numbers Real Numbers Algebra

Polynomial Functions Card Sort Video Polynomials Polynomial Functions Sorting Cards

Subsets Of Real Numbers Ck 12 Foundation

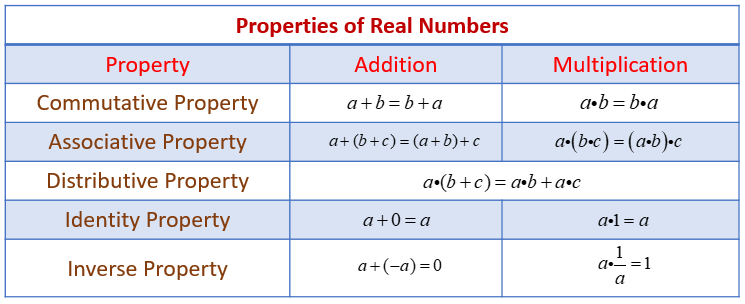
Real Numbers And Their Operations

Pin On Interactive Notes

The Radical Square Root Complex Numbers Rational Numbers Radical Equations

I Really Like The Different Ideas For Concept Mapping In Math Classes Math Fun Math Math Class

Solving Linear Inequalities Digital Bundle Distance Learning Video Technology Lessons Distance Learning Math Lessons